L2 Calculus
Question Bank
Question: The function $f(x) = kx^3 + 9x$ has a tangent with a gradient of 15 at the point where $x=2$. Find the value of k.
Derivative $f'(x) = 3kx^2 + 9$. Set $f'(2) = 15$: $3k(2)^2 + 9 = 15 \implies 12k = 6 \implies k = 0.5$.
Question: Use calculus to show that the line $y = 4x - 3$ is a tangent to the graph of the function $f(x) = x^2 + 6x - 2$.
Step 1: Find the derivative of the function $f(x)$ to get the gradient function.
$f'(x) = 2x + 6$
Step 2: The gradient of the line $y=4x-3$ is 4. Find the x-coordinate where the function's gradient is also 4.
$2x + 6 = 4 \implies 2x = -2 \implies x = -1$.
Step 3: Find the y-coordinate on the curve at this point by substituting $x=-1$ into the original function, $f(x)$.
$f(-1) = (-1)^2 + 6(-1) - 2 = 1 - 6 - 2 = -7$.
The point of tangency on the curve is $(-1, -7)$.
Step 4: Check if this point also lies on the line $y = 4x - 3$.
$y = 4(-1) - 3 = -4 - 3 = -7$.
Since the point $(-1, -7)$ is on both the curve and the line, and their gradients are equal at that point, the line is a tangent.
Question: Use calculus to find the value of $k$ if the line $y = 7x + k$ is a tangent to the graph of the function $f(x) = 2x^2 - 5x + 3$.
Step 1: At the point of tangency, the gradient of the function must be equal to the gradient of the tangent line. From the equation $y=7x+k$, the gradient of the tangent line is 7.
Step 2: Find the derivative of the function $f(x)$ to get the gradient function.
$f'(x) = 4x - 5$
Step 3: Set the derivative equal to the gradient of the tangent line to find the x-coordinate of the point of tangency.
$4x - 5 = 7 \implies 4x = 12 \implies x = 3$.
Step 4: Substitute this x-value back into the original function, $f(x)$, to find the y-coordinate of the point of tangency.
$f(3) = 2(3)^2 - 5(3) + 3 = 18 - 15 + 3 = 6$.
The point of tangency is $(3, 6)$.
Step 5: Since the point of tangency lies on the tangent line, substitute its coordinates into the line's equation, $y=7x+k$, to solve for $k$.
$6 = 7(3) + k \implies 6 = 21 + k \implies k = -15$.
The value of $k$ is -15.
Question: A tangent to the graph of the function $f(x) = -2x^2 + 8x - 3$ has a gradient of -4, and passes through the point $(a, -1)$, where $a$ is a constant. Find the value of $a$.
Step 1: Differentiate the function to find the gradient function, $f'(x)$.
$f'(x) = -4x + 8$
Step 2: Set the gradient function equal to the given gradient (-4) to find the x-coordinate of the point of tangency.
$-4x + 8 = -4 \implies 12 = 4x \implies x = 3$.
Step 3: Substitute this x-value back into the original function, $f(x)$, to find the y-coordinate of the point of tangency.
$f(3) = -2(3)^2 + 8(3) - 3 = -18 + 24 - 3 = 3$.
The point of tangency is $(3, 3)$.
Step 4: Determine the equation of the tangent line using the point-gradient formula, $y - y_1 = m(x - x_1)$.
$y - 3 = -4(x - 3)$
$y - 3 = -4x + 12 \implies y = -4x + 15$.
Step 5: The tangent line passes through the point $(a, -1)$. Substitute these coordinates into the tangent line's equation to solve for $a$.
$-1 = -4(a) + 15 \implies -16 = -4a \implies a = 4$.
The value of $a$ is 4.
Question: An open box container is made for production. The container must have a volume of 32 m³. Use calculus to find the minimum possible surface area of the container.
Step 1: Define variables and set up the equations for Volume (V) and Surface Area (A). Let the square base have side length $x$ and the height be $h$.
Volume: $V = x^2h = 32$
Surface Area (open top): $A = \text{Area of base} + \text{Area of 4 sides} = x^2 + 4xh$
Step 2: Use the volume equation to express $h$ in terms of $x$, then substitute it into the area equation to get a function of a single variable, $A(x)$.
From the volume equation, $h = \frac{32}{x^2}$.
$A(x) = x^2 + 4x(\frac{32}{x^2}) = x^2 + \frac{128}{x}$
Step 3: Differentiate $A(x)$ to find the gradient function. First, write the function with a negative exponent: $A(x) = x^2 + 128x^{-1}$.
$A'(x) = 2x - 128x^{-2} = 2x - \frac{128}{x^2}$
Step 4: To find the minimum area, set the derivative to zero and solve for $x$.
$2x - \frac{128}{x^2} = 0 \implies 2x = \frac{128}{x^2} \implies 2x^3 = 128 \implies x^3 = 64 \implies x = 4$.
The minimum surface area occurs when the base side length is 4 m.
Step 5: Substitute $x=4$ back into the surface area function to find the minimum area.
$A(4) = (4)^2 + \frac{128}{4} = 16 + 32 = 48$.
The minimum possible surface area is 48 m².
Question: A rectangle is drawn inside the parabola $y = c - x^2$ so that two of its vertices lie on the x-axis, and two of its vertices lie on the parabola, as shown in the diagram.
Show that the area of the rectangle is maximised when the width of the rectangle is $2\sqrt{\frac{c}{3}}$.
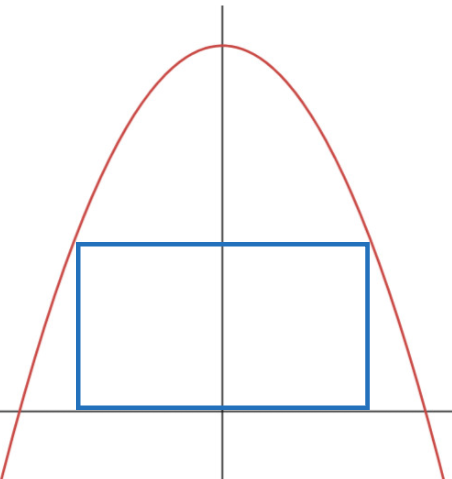
Step 1: Define the dimensions of the rectangle. If the top-right vertex is at the point $(x, y)$, then due to symmetry, the width of the rectangle is $2x$ and the height is $y$.
The Area, $A$, is given by $A = \text{width} \times \text{height} = (2x)(y)$.
Step 2: Substitute the parabola's equation, $y = c - x^2$, into the area formula to express the area as a function of a single variable, $x$.
$A(x) = 2x(c - x^2)$
$A(x) = 2cx - 2x^3$
Step 3: To find the maximum area, differentiate $A(x)$ with respect to $x$.
$A'(x) = 2c - 6x^2$
Step 4: Set the derivative equal to zero to find the value of $x$ that gives a stationary point (in this case, the maximum).
$2c - 6x^2 = 0 \implies 2c = 6x^2 \implies x^2 = \frac{c}{3}$
$x = \sqrt{\frac{c}{3}}$ (since x must be a positive length).
Step 5: The question asks for the width of the rectangle, which is $2x$.
Width = $2 \times x = 2\sqrt{\frac{c}{3}}$
This shows that the area is maximised when the width is $2\sqrt{\frac{c}{3}}$.
Question: The profit, $\$P$, from selling $x$ items is modelled by $P(x) = 2x^2 + 50x - 300$. Find how many items are being sold when the rate of change of profit is $\$70$ per item.
Step 1 (Differentiate): The rate of change of profit is the derivative, $P'(x)$.
$$P'(x) = 4x + 50$$Step 2 (Solve for x): Set the rate of change equal to 70 and solve for $x$.
$$4x + 50 = 70$$ $$4x = 20$$ $$x = 5$$5 items are being sold.
Question: Air is being pumped into a spherical balloon. The radius, $r$, is increasing at a constant rate of 0.5 cm/s and has an initial radius of 1 cm. This means the radius at time $t$ seconds is given by the formula $r = 0.5t + 1$.
Find the rate at which the volume, $V$, is increasing at the instant when the radius is 4 cm. (Note: $V = \frac{4}{3}\pi r^3$)
Step 1: First, find the time, $t$, when the radius is 4 cm.
$4 = 0.5t + 1 \implies 3 = 0.5t \implies t = 6$ seconds.
Step 2: To find the rate of change of volume with respect to time ($\frac{dV}{dt}$), express the volume $V$ as a function of time $t$. Substitute the expression for $r$ into the volume formula.
$V(t) = \frac{4}{3}\pi (0.5t + 1)^3$
Step 3: Expand the cubic term $(0.5t + 1)^3$.
$(0.5t + 1)^3 = 0.125t^3 + 0.75t^2 + 1.5t + 1$.
This gives the full expression for $V(t) = \frac{4}{3}\pi (0.125t^3 + 0.75t^2 + 1.5t + 1)$.
Step 4: Differentiate $V(t)$ with respect to $t$ to find the rate of change.
$\frac{dV}{dt} = \frac{4}{3}\pi (0.375t^2 + 1.5t + 1.5)$
Step 5: Substitute $t=6$ into the derivative to find the rate at that instant.
At $t=6$, $\frac{dV}{dt} = \frac{4}{3}\pi (0.375(6)^2 + 1.5(6) + 1.5)$
$\frac{dV}{dt} = \frac{4}{3}\pi (13.5 + 9 + 1.5) = \frac{4}{3}\pi (24) = 32\pi$.
The volume is increasing at a rate of $32\pi$ cm³/s.